Python Dilinde SciPy Diferansiyel Evrim Nedir?
Scipy, bilimsel ve matematiksel sorunları çözmek için kullanılan yüzeysel, ücretsiz ve anlaşılır bir kütüphanedir. SciPy, geliştiriciler için bir hazine kutusudur çünkü kütüphanesi değerli modüllerle doludur. SciPy, NumPy işlevselliğini değerli bir algoritma kümesiyle genişletir. SciPy kitaplığı, scipy.io, scipy.optimize gibi hesaplamalar için kullanılabilecek alt paketlere sahiptir. SciPy, scipy.optimize paketinde bir 'diferansiyel evrim' işlevi ve birçok güçlü işlev üretir. scipy.optimize, Python uygulamalarında optimizasyon için kullanılır.
Diferansiyel Evrim Fonksiyonu, çok değişkenli fonksiyonların global minimumunu bulmak için kullanılan SciPy optimize paketi tarafından elde edilen global bir fonksiyondur. Doğrusal olmayan ve türevlenemeyen çok boyutlu amaç fonksiyonlarını yönetebilir. Sürekli uzay fonksiyonlarının alanlarını aramak için kullanılan bir arama algoritmasıdır. Bu fonksiyon gerçek değerler üzerinde çalışır.
Diferansiyel Evrim Fonksiyonunun Sözdizimi
Diferansiyel evrim işlevi, Python'da diferansiyel_evolution () işlevini kullanan mevcuttur. Diferansiyel evrim fonksiyonunun sözdizimi aşağıda gösterilmiştir:
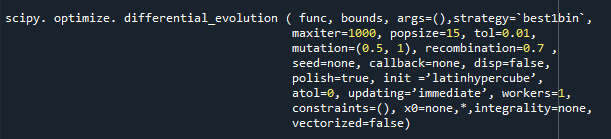
Şimdi fonksiyon parametrelerini gözden geçirelim:
İşlev, f(x,*args); ile çağrılabilir olmalıdır; sınırlar, iki şekilde belirtilebilen değişken dizisini ifade eder: strateji isteğe bağlıdır veya 'best1bin' varsayılan değerine sahip bir dizedir; maxiter isteğe bağlıdır veya bir int değeridir; popsize int veya isteğe bağlıdır; tol int veya isteğe bağlıdır; mutasyon değeri değişken veya isteğe bağlıdır; rekombinasyon değeri değişken veya isteğe bağlıdır; tohum yok, int, NumPy ve Random'dır.
Bir sonraki bölümde, kolay örneklerin yardımıyla bir diferansiyel evrim fonksiyonunu tartışacağız.
örnek 1
Diferansiyel evrim fonksiyonu kavramını anlama konusundaki ilginizi geliştirecek basit bir örnekle başlayalım. Minimum değeri bulmak için diferansiyel_evolution() işlevini kullandık. Ancak, minimum değeri bulmak için, işlev arama sınırlarını ve tanımlanmış bir çağrılabilir amaç işlevini gerektiriyordu. Sonuç olarak diferansiyel_evolution fonksiyonunu programda kullanmadan önce bir fonksiyon tanımlıyoruz. Programın referans kodu aşağıda belirtilmiştir:
içe aktarmak dizi olarak Örneğin.itibaren keskin içe aktarmak optimize etmek
itibaren keskin. optimize etmek içe aktarmak diferansiyel_evrim
içe aktarmak matplotlib. çizim planı olarak py
itibaren matplotlib içe aktarmak santimetre
kesinlikle işlev ( p ) :
ile birlikte , x = p
h = Örneğin. sqrt ( ile birlikte ** 4 + x ** 4 )
geri dönmek Örneğin. sqrt ( h )
DE_sınırları = [ [ - 6 , 6 ] , [ - 6 , 6 ] ]
res = diferansiyel_evrim ( işlev , DE_sınırları )
Yazdır ( res )
Dizi sayısal hesaplamaları için SciPy ve NumPy gibi kütüphaneleri içe aktardık. scipy.optimize modülünden diferansiyel_evolution fonksiyonunu içe aktardık. Daha sonra “def” anahtar kelimesi ile çağrılabilir amaç fonksiyonunu tanımlayıp “p” parametresini geçiyoruz. NumPy değişkenleri toplamının karekökünü bulan fonksiyonu yani z, x'i başarıyla tanımlıyoruz. Karekök değeri “h” değişkeninde saklanır. Tanımlanan işlevde karekök değerini döndürürüz. Argüman olarak döndürülür.
Daha sonra fonksiyonun min ve max değerlerini açıklayarak değişkenin maddeleştirilebilecek sınırlarını belirliyoruz. Argüman olarak 'DE_bounds' ile diferansiyel_evolution işlevini yürütürüz. Res adında bir değişkenle fonksiyon değerini çağırdık. Son olarak, çıktıyı göstermek için print deyimini kullanırız. Sonuç, programı çalıştırdıktan sonra görüntülendi. Beklenen çıktı ekran görüntüsü aşağıda gösterilmiştir:
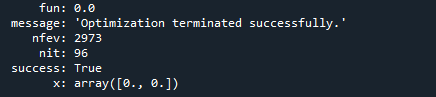
Differential_evolution() işlevin minimum değerinin (0, 0) noktasında görüntülendiğini gösterir.
Örnek 2
Bu, diferansiyel evrim fonksiyonunun başka bir örneğidir. Bunda dizileri alıp aralarında farklı işlemler uyguluyoruz. Programın referans kodu aşağıda belirtilmiştir:
içe aktarmak dizi olarak Örneğin.itibaren keskin içe aktarmak optimize etmek
itibaren keskin. optimize etmek içe aktarmak diferansiyel_evrim
kesinlikle amaç_func ( d ) :
geri dönmek ( d [ 1 ] - 1.2 ) / 2 + 0,5 * d [ 0 ] * 1.3 * ( d [ 1 ] + 0,5 ) ** 3
_sınır = [ ( - 0.3 , 0.3 ) , ( - 0.3 , 0.3 ) ]
disp = diferansiyel_evrim ( amaç_func , _sınır , popsize = 80 , Lehçe = YANLIŞ )
Yazdır ( disp )
Önceki ekran görüntüsünde gösterildiği gibi, SciPy.optimize.differential_evolution kitaplığını ve NumPy kitaplığını programa başarıyla aktardık. Şimdi adına bir minimum değer bulduğumuz bir amaç fonksiyonu tanımlıyoruz. Matematiksel ifadeyi amaç fonksiyonunda geçirdik ve tanımlanan fonksiyona argüman olarak bir değer döndürdük. Fonksiyon değerleri arasındaki sınır bir zorunluluktur. Böylece, işlevi tanımladıktan sonra, her iki değeri de (maksimum ve minimum) sabitledik.
Tüm temel değişkenleri tanımladıktan sonra, bir fonksiyonun minimum değerini bulmak için diferansiyel_evolution fonksiyonunu çağırdık. Fonksiyonun minimum dönüş değerini disp adlı bir değişkene kaydettik. Programın sonunda, sonucu görüntülemek için print ifadesinde disp değişkenini geçiyoruz. Programı çalıştırdıktan sonra, tanımlanan fonksiyonun minimum değeri sınırlarla ekranda görüntülenir. Aşağıdaki çıktı:
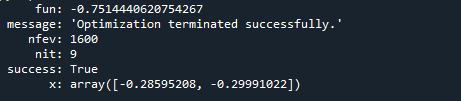
Örnek 3
Gördüğümüz gibi, diferansiyel evrim, tanımına bağlı olarak bir amaç fonksiyonunun farklı minimum değerlerini verir. Burada, diferansiyel_evolution() ile ilgili başka bir örnek alıyoruz. Bu programın referans kodu aşağıda gösterilmiştir:
içe aktarmak dizi olarak Örneğin.itibaren keskin içe aktarmak optimize etmek
itibaren keskin. optimize etmek içe aktarmak diferansiyel_evrim
kesinlikle obj_func ( operatör ) :
geri dönmek 3 ** 9 / 0.2 + 6 / 3 * 2 ** yirmi
sınır = [ ( - 0,5 , 0,5 ) , ( - 0,5 , 0,5 ) ]
dışarı = diferansiyel_evrim ( obj_func , sınır , Lehçe = Doğru )
Yazdır ( 'Çıktı:' , dışarı )
Kitaplıklar bu programa başarılı bir şekilde aktarılmıştır çünkü onlar olmadan istediğimiz işlemleri yapamayız. Sonuç olarak SciPy kütüphanesini programa dahil ediyoruz. Bundan sonra, amaç fonksiyonunu gerekli işlemle tanımlayın. Tanımlanan fonksiyonun minimum değerini buluyoruz. Fonksiyonun sınırını ayarladıktan sonra, fonksiyonun minimum değerini bulmak için tanımlı fonksiyonu diferansiyel evrimde çağırdık. Bu daha sonra değişkende tutulur. Bunu print ifadesinde bu değişkeni çağırarak gösteriyoruz. Bu programın çıktısı aşağıda gösterilmiştir:
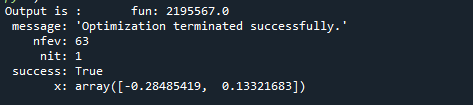
Önceki ekran görüntüsünde olduğu gibi, işlevin minimum değeri [0.29236931, 0.16808904] şeklindedir. Diferansiyel_evrim işlevi kavramını daha iyi anlamak için bu örnekleri ortamınızda da çalıştırabilirsiniz.
Çözüm
Bu makalenin hızlı bir özetini yapalım. Python'da SciPy kütüphanesine ait olan diferansiyel evrim yönteminin temel fonksiyonlarını kavradık. Python, çok sayıda esnek kitaplığa sahip en yeni dildir. Çoğu geliştiriciye, önceden tanımlanmış işlevler ve kitaplıklar tarafından karmaşık kod yapılarını çözmede yardım edildi. Diferansiyel evrim, minimizasyon için kullanılan bir SciPy paket optimizasyon işlevi veya yöntemidir. Bu önceki örnekleri kodda kullandığınızda, diferansiyel evrim kavramını daha net anlarsınız.